0545:二叉树的边界(★)
目录
题目
二叉树的 边界 是由 根节点 、左边界 、按从左到右顺序的 叶节点 和 逆序的右边界 ,按顺序依次连接组成。
左边界 是满足下述定义的节点集合:
- 根节点的左子节点在左边界中。如果根节点不含左子节点,那么左边界就为 空 。
- 如果一个节点在左边界中,并且该节点有左子节点,那么它的左子节点也在左边界中。
- 如果一个节点在左边界中,并且该节点 不含 左子节点,那么它的右子节点就在左边界中。
- 最左侧的叶节点 不在 左边界中。
右边界 定义方式与 左边界 相同,只是将左替换成右。即,右边界是根节点右子树的右侧部分;叶节点 不是 右边界的组成部分;如果根节点不含右子节点,那么右边界为 空 。
叶节点 是没有任何子节点的节点。对于此问题,根节点 不是 叶节点。
给你一棵二叉树的根节点 root ,按顺序返回组成二叉树 边界 的这些值。
示例 1:
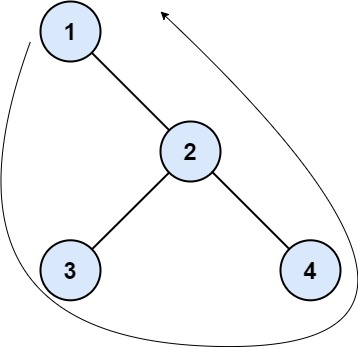
输入:root = [1,null,2,3,4] 输出:[1,3,4,2] 解释: - 左边界为空,因为二叉树不含左子节点。 - 右边界是 [2] 。从根节点的右子节点开始的路径为 2 -> 4 ,但 4 是叶节点,所以右边界只有 2 。 - 叶节点从左到右是 [3,4] 。 按题目要求依序连接得到结果 [1] + [] + [3,4] + [2] = [1,3,4,2] 。
示例 2:
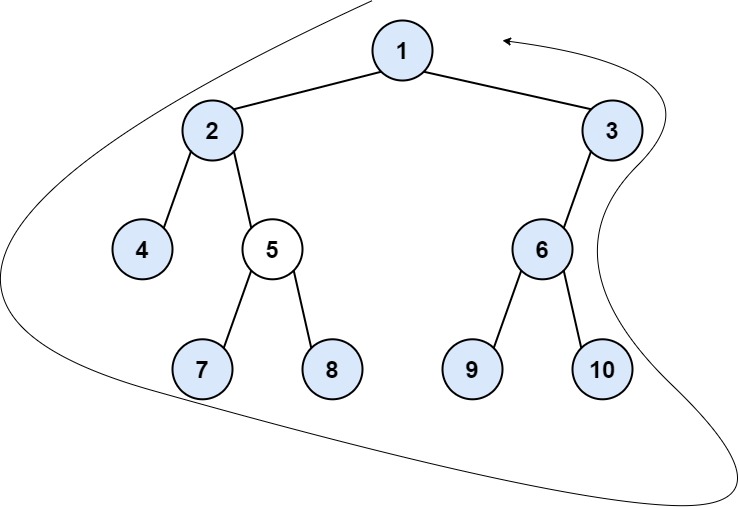
输入:root = [1,2,3,4,5,6,null,null,null,7,8,9,10] 输出:[1,2,4,7,8,9,10,6,3] 解释: - 左边界为 [2] 。从根节点的左子节点开始的路径为 2 -> 4 ,但 4 是叶节点,所以左边界只有 2 。 - 右边界是 [3,6] ,逆序为 [6,3] 。从根节点的右子节点开始的路径为 3 -> 6 -> 10 ,但 10 是叶节点。 - 叶节点从左到右是 [4,7,8,9,10] 按题目要求依序连接得到结果 [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3] 。
提示:
- 树中节点的数目在范围
[1, 104]内 -1000 <= Node.val <= 1000
分析
模拟分别遍历得到左边界、右边界、顺序的叶子节点即可。
解答
|
|
48 ms