0351：安卓系统手势解锁（★）

2015-12-17 约 960 字预计阅读 2 分钟次阅读

力扣第 351 题

题目

我们都知道安卓有个手势解锁的界面，是一个 3 x 3 的点所绘制出来的网格。用户可以设置一个 “解锁模式” ，通过连接特定序列中的点，形成一系列彼此连接的线段，每个线段的端点都是序列中两个连续的点。如果满足以下两个条件，则 k 点序列是有效的解锁模式：

解锁模式中的所有点 互不相同 。
假如模式中两个连续点的线段需要经过其他点的中心，那么要经过的点 必须提前出现 在序列中（已经经过），不能跨过任何还未被经过的点。
- 例如，点 5 或 6 没有提前出现的情况下连接点 2 和 9 是有效的，因为从点 2 到点 9 的线没有穿过点 5 或 6 的中心。
- 然而，点 2 没有提前出现的情况下连接点 1 和 3 是无效的，因为从圆点 1 到圆点 3 的直线穿过圆点 2 的中心。

以下是一些有效和无效解锁模式的示例：

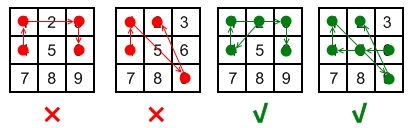
无效手势：[4,1,3,6] ，连接点 1 和点 3 时经过了未被连接过的 2 号点。
无效手势：[4,1,9,2] ，连接点 1 和点 9 时经过了未被连接过的 5 号点。
有效手势：[2,4,1,3,6] ，连接点 1 和点 3 是有效的，因为虽然它经过了点 2 ，但是点 2 在该手势中之前已经被连过了。
有效手势：[6,5,4,1,9,2] ，连接点 1 和点 9 是有效的，因为虽然它经过了按键 5 ，但是点 5 在该手势中之前已经被连过了。

给你两个整数，分别为 m 和 n ，那么请返回有多少种 不同且有效的解锁模式 ，是至少需要经过 m 个点，但是 不超过 n 个点的。

两个解锁模式不同需满足：经过的点不同或者经过点的顺序不同。

示例 1：

输入：m = 1, n = 1
输出：9

示例 2：

输入：m = 1, n = 2
输出：65

提示：

1 <= m, n <= 9

分析

#1

数据较小，可以直接生成所有可能的排列，判断是否有效即可：

本题中，若两点连线经过其它点，必然是这两点的中点
因此判断两个连续点的中点是否为网格、是否已访问即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


def numberOfPatterns(self, m: int, n: int) -> int:
    def check(A):
        vis = set()
        for a, b in pairwise(A):
            x1, y1 = divmod(a, 3)
            x2, y2 = divmod(b, 3)
            mid = (x1+x2)//2*3+(y1+y2)//2
            if (x1+x2)%2==0 and (y1+y2)%2==0 and mid not in vis:
                return False
            vis.add(a)
        return True
    return sum(check(A) for k in range(m, n+1) for A in permutations(range(9), k))

时间复杂度 O(9 * 9!)，3884 ms

#2

还可以用状压 dp。

令 dp[st][i] 代表访问过的点集合是 st 且最后一个点是 i 的有效序列数量，即可递推。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


def numberOfPatterns(self, m: int, n: int) -> int:
    def check(st, i, j):
        x1, y1 = divmod(i, 3)
        x2, y2 = divmod(j, 3)
        mid = (x1+x2)//2*3+(y1+y2)//2
        return (x1+x2)%2 or (y1+y2)%2 or st&(1<<mid)

    res, dp = 0, [[0]*9 for _ in range(1<<9)]
    for i in range(9):
        dp[1<<i][i] = 1
    for st in range(1<<9):
        for i in range(9):
            for j in range(9):
                if not st&(1<<j) and check(st, i, j):
                    dp[st|(1<<j)][j] += dp[st][i]
    return sum(sum(dp[st]) for st in range(1<<9) if m<=bin(st).count('1')<=n)

时间复杂度 O(9 * 9 * 2^9)，352 ms

目录

0351：安卓系统手势解锁（★）

题目

分析

#1

#2

解答