0276:栅栏涂色(★)
目录
题目
有 k 种颜色的涂料和一个包含 n 个栅栏柱的栅栏,请你按下述规则为栅栏设计涂色方案:
- 每个栅栏柱可以用其中 一种 颜色进行上色。
- 相邻的栅栏柱 最多连续两个 颜色相同。
给你两个整数 k 和 n ,返回所有有效的涂色 方案数 。
示例 1:
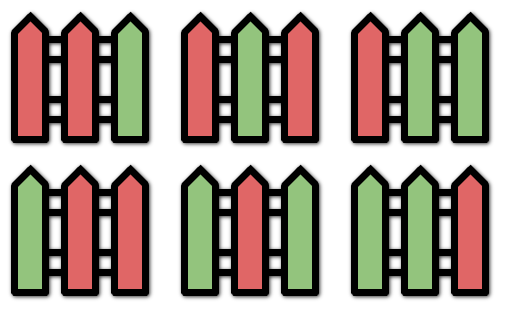
输入:n = 3, k = 2 输出:6 解释:所有的可能涂色方案如上图所示。注意,全涂红或者全涂绿的方案属于无效方案,因为相邻的栅栏柱 最多连续两个 颜色相同。
示例 2:
输入:n = 1, k = 1 输出:1
示例 3:
输入:n = 7, k = 2 输出:42
提示:
1 <= n <= 501 <= k <= 105- 题目数据保证:对于输入的
n和k,其答案在范围[0, 231 - 1]内
分析
典型的 dp,令 dp[i][0] 代表前 i 个栅栏最后两个不连续的涂色方案数, dp[i][1] 代表前 i 个栅栏最后两个连续的涂色方案数,即可递归。
因为 dp[i] 只依赖于 dp[i-1],所以可以优化为两个参数。
解答
|
|
36 ms
*附加
这是完全的线性递推关系,因此可以用矩阵快速幂优化。
|
|
96 ms