0240：搜索二维矩阵 II（★）

2015-08-28 约 477 字预计阅读 1 分钟次阅读

力扣第 240 题

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

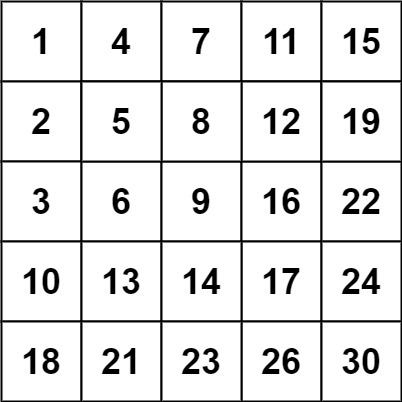
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-10⁹ <= matrix[i][j] <= 10⁹
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-10⁹ <= target <= 10⁹

相似问题：

0074：搜索二维矩阵

分析

最简单的就是遍历每行，二分查找即可
注意到每行二分查找到的位置 j 是递减的
因此令 j 初始在最右边，遍历每行并移动 j，即可线性时间完成

解答

1
2
3
4
5
6
7
8
9


class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        j = len(matrix[0])-1
        for row in matrix:
            while j>=0 and row[j]>target:
                j -= 1
            if row[j]==target:
                return True
        return False

153 ms

*附加

还可以考虑直接对矩阵二分：

先在第 i=m//2 行二分查找到第一个 >=target 的位置 j，假如不等于 target
矩形 <0,0,i,j-1> 内的元素必然 < target
矩形 <i, j, m-1, n-1>)内的元素必然大于 target
只用再搜索矩形 <i+1, 0,m-1, j-1> 和矩形 <0, j, i-1, n-1> 即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        def dfs(x1, y1, x2, y2):
            if x1>x2 or y1>y2:
                return False
            i = (x1+x2)//2
            j = bisect_left(matrix[i], target, y1, y2+1)
            if j<=y2 and matrix[i][j]==target:
                return True
            return dfs(i+1,y1,x2,j-1) or dfs(x1,j,i-1,y2)

        m, n = len(matrix), len(matrix[0])
        return dfs(0,0,m-1,n-1)

时间 $O(log(M*N))$，159 ms

目录

0240：搜索二维矩阵 II（★）

题目

分析

解答

*附加

解答